Trường Đại học Zurich, Thụy Sỹ

Đại học Sư phạm Thái Nguyên 17/09/2017

 

          Được sự đồng ý của Đảng ủy, Ban Giám hiệu trường Đại học Sư phạm-Đại học Thái Nguyên, Khoa Toán đã mời Giáo sư Markus Brodmann, trường Đại học Zurich, Thụy Sỹ giảng bài giảng đại chúng về chủ đề “Tại sao bạn lại trở thành một nhà toán học?” (Why to become a mathematician?) và làm việc với nhóm nghiên cứu Đại số.

Bài giảng đại chúng có nội dung hấp dẫn với nhiều hoạt động trải nghiệm. Cấu trúc bài báo cáo là sự chuẩn mực cho các nhà sư phạm tham khảo. Bài báo cáo được chia làm bảy phần với nội dung phong phú. Đặc biệt trong báo cáo, giáo sư cho ta thấy mối liên hệ giữa toán học với những sự vật, sự việc xuất hiện trong đời thường đến trí tưởng tượng phong phú của các nhà toán học. Ở phần này giáo sư bắt đầu bằng hình ảnh dải Moebius (Moebius strip). Từ việc quan sát thực tế giáo sư nhấn mạnh đến việc phát triển trí tưởng tượng trong toán học, biết dự đoán điều gì sẽ xảy ra (Guess first what comes out).

Dải Moebius có nhiều ứng dụng trong âm nhạc, vật lý, điện công nghệ, hóa học, công nghệ nano, kiến trúc. Việc quan sát cũng bắt đầu từ những tính chất đơn giản (cắt, số mặt) đến những tính chất phức tạp hơn (định hướng). Đỉnh điểm của sự tưởng tưởng là chai Klein (Klein Bottle).

Trong toán học, chai Klein (hay bình Klein) là một ví dụ cho mặt không định hướng, nói cách khác, đó là một bề mặt (một đa tạp hai chiều), mà trong đó khái niệm về trái và phải không thể được xác định một cách nhất quán. Một số khái niệm hình học không định hướng liên quan khác có thể kể tới như mặt Mobius hay mặt phản xạ thực. Đối với dải Mobius, đây là một bề mặt có biên, còn chai Klein thì không có biên.

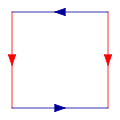
Chai Klein được cấu thành từ một hình vuông, nếu dán cạnh có màu tương ứng với nhau, theo hình minh hoạ bên dưới.

  Nói rõ hơn, chai Klein là không gian thương được mô tả như hình vuông [0,1] × [0,1] với các cạnh bên xác định bởi quan hệ (0, y) ~ (1, y) với 0 ≤ y ≤ 1 và (x, 0) ~ (1 − x, 1) với 0 ≤ x ≤ 1: Hình vuông này là một đa giác cơ sở của chai Klein. Lưu ý rằng: chúng ta nói đến việc "dán" ở đây là theo nghĩa trừu tượng để dễ hiểu trong một không gian 3 chiều, và kết quả là ta có thể hình dung được 1 chai Klein tự giao. Tất nhiên chai Klein không giao nhau. Tuy nhiên, có một cách để hình dung chai Klein trong không gian bốn chiều.

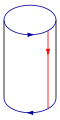
Dán các cạnh có mũi tên màu đỏ trên hình vuông vào với nhau, để tạo thành một hình trụ. Tiếp theo, dán hai cạnh còn lại, mỗi cái lại tạo thành một hình trụ. Chú ý, ta sẽ tạo ra một hình tròn tự giao nhau. Đây là một phép nhúng của chai Klein trong không gian ba chiều.

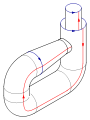
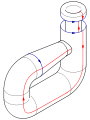
Bằng việc thêm chiều thứ 4 vào không gian 3 chiều, sự tự giao có thể được loại bỏ. Nhẹ nhàng đẩy một phần của ống có chứa phần giao dọc theo chiều thứ tư, ra khỏi không gian 3 chiều ban đầu. Một trường hợp tương tự có lợi khi xem xét một đường cong tự giao trên mặt phẳng; phần giao có thể được loại bỏ bằng cách nâng một phần ra khỏi mặt phẳng.

Phép nhúng này rất hữu ích cho việc hình dung các tính chất của chai Klein. Ví dụ, chai Klein không biên, bề mặt có chỗ dừng lại đột ngột, và không định hướng, được phản xạ từ một phía của mặt nhúng.

Để nghiên cứu những tính chất quan sát được ta phải dùng những công cụ của Toán học. Những gợi ý Toán học của giáo sư tạo hứng khởi cho các em sinh viên nghiên cứu.

Sau khi giới thiệu những vấn đề “nổi cộm” khác của Toán, giáo sư đưa ra mối liên hệ của Toán với khoa học và kỹ thuật cũng như những ứng dụng của Toán học. Những giới thiệu của giáo sư khiến những người không nghiên cứu Toán cũng cảm thấy Toán học thật hữu dụng và gần gũi.

Bức tranh Toán học đương thời cũng được giáo sư phác họa hết sức sôi động (Mathematics is a very broad field with many domains of specialization). Để trở thành những nhà toán học hay những người dạy toán giáo sư khuyên chúng ta cần phải:

- Willingness to Work Hard (Sẵn sàng làm việc chăm chỉ);

- Imagination (Có trí tưởng tượng);

- Ability to Love Abstract Thinking (Có khả năng yêu thích tư duy trừu tượng);

- Intellectual Curiosity (Có tính tò mò, ham hiểu biết);

- Sense for Strict Reasoning and Logical Arguments (Có khả năng lập luận chặt chẽ và suy luận logic);

- Ability to Communicate (Có khả năng truyền đạt);

- Common Sense (Có khả năng chia sẻ).

Cuối cùng giáo sư đưa ra những lý do sau khiến ta yêu Toán hơn và những giáo viên dạy Toán, những người nghiên cứu Toán gắn bó hơn, có trách nhiệm hơn với nghề nghiệp của mình:

- Toán học thật năng động, đầy thử thách và thú vị, cho bạn niềm đam mê khám phá;

- Toán học là một trong những ngành khoa học chính xác nhất, và nó hình thành tư duy cho bạn; Bạn hoàn toàn có thể làm toán ở bất kì đâu chỉ bằng một chiếc bút và mảnh giấy;

- Toán học là chìa khóa của công nghệ, khoa học và kỹ thuật, vì vậy những đóng góp của bạn luôn có ý nghĩa thực tiễn lớn lao;

- Thật dễ dàng tìm thấy ngôn ngữ chung trong toán học, đó là lý do bạn có thể hòa mình vào cộng đồng toán học toàn cầu, ở đó bạn luôn được chia sẻ những ý tưởng và khám phá;

- Toán học được coi là gốc rễ, nguồn cội của sự phát triển khoa học, kỹ thuật và vì thế những công hiến của bạn sẽ đóng góp vào sự phát triển của đất nước bạn;

- Dạy toán cũng vô cùng thú vị, khi là một giáo viên dạy toán, bạn đã đóng góp nhiều cho sự phát triển của xã hội.

Cuối bài giảng giáo sư giao lưu với giảng viên, sinh viên, học viên cao học và nghiên cứu sinh của khoa về giáo dục Thụy Sỹ, về những chia sẻ của giáo sư trong việc dạy Toán, nghiên cứu Toán, …. Những trao đổi của giáo sư rất bổ ích cho thày trò khoa Toán, cũng như nhà trường trong việc nâng cao năng lực nghiên cứu khoa học, hợp tác, quan hệ quốc tế, đổi mới và phát triển chương trình đào tạo giáo viên;  tìm kiếm cơ hội du học cho cán bộ, sinh viên; đặc biệt tạo hứng khởi cho sinh viên K52 học tập, nghiên cứu.

Buổi chiều giáo sư làm việc với nhóm nghiên cứu Đại số, học viên cao học và nghiên cứu sinh.

Một số hình ảnh trong buổi giảng bài:

 

Nguồn: Khoa Toán